Write Up 11: Polar Equations

Zachary Laughlin

Introduction:

Throughout this write-up, we will be discussing equations in polar form. The difference in a polar equation is that our outputs and inputs are defined differently. We are used to writing our equations with an x-input and a y-output. But in the polar plane, equations are defined with an input value of - the angle measure swept out from due east, and a output value of r- radius of the circle defined in the plane.

Investigation 1:

For the first investigation, suppose we are working with the polar equations:

in this investigation, we will keep everything constant except the value of "k." Throughout this first investigation, we will change the value of "k" and see how this variable in the polar equation varies. Therefore, suppose we start with the polar equations below and their graphs:

We can see from the graph above that the added value of 1 makes a big difference in the polar equation. When k=2, the polar equation r=1+cos(2) represented by the purple graph gives us some sort of bow tie with two connecting egg shaped figures. The other polar equation r=cos(2theta) represented by the red graph gives us a four leaf clover; which is very different from the purple graph. The only similarity between the two polar graphs is that both the x-axis and y-axis act as axes of symmetry for both graphs.

What if "k" is odd? Lets say k=3:

When k=3, the two graph looks very similar. The graph of r=1+cos(3) acts as some sort of geometrical dilation of the graph r=cos(3). It seems as if the added 1 acts as a scale factor for the graph. Both graphs share the same connective point where all three cloves meet and both graph share the same axes of symmetry. One being the x-axis and the other being some line y=-cx where c is some constant.

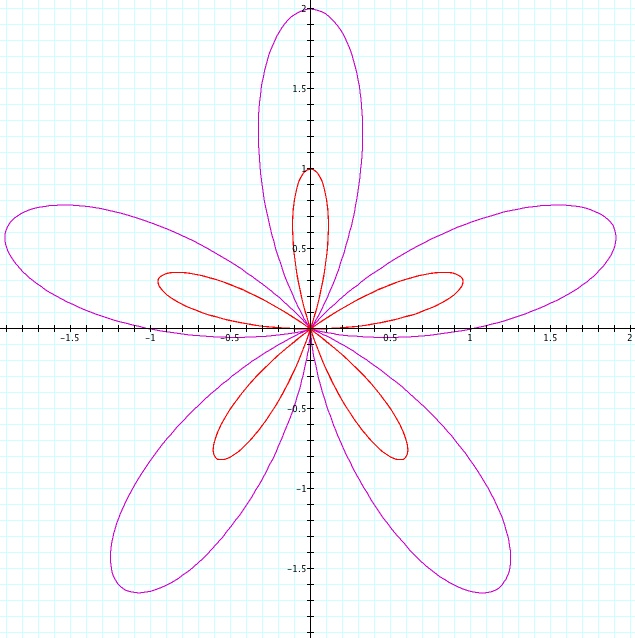
Suppose k=4:

When k=4, the polar equation r=1+cos(4) produces a four-leaf clover with its' minimum and maximums reaching 2 and -2 on the x & y axes. Our other equation r=cos(4) produces an eight-leaf clover with its min's and max's reaching 1 and -1 on the x & y axes. Therefore, not only has the equation with the additive 1 double in size, it has also lost four cloves. This seems to be the trend for even values for "k." When k=2 and k=4, the equation will the additive 1, [r=1+cos(2)] ,was twice as big and had half the cloves compared to the polar equation without an additive 1, [r= cos(2)].

Suppose k=5:

The trend also continues for odd values of k. The orientation of both graphs are congruent. Both graphs contain 5 cloves all connecting at the origin of the plane. Again, the added value of 1 in the equation r=1+cos(5) has dilated the figure by some scale factor making it bigger than the polar equation without the added 1, r=cos(5). They both share the same axes of symmetry with one being the x-axis and the other be some line y=cx where is some constant.

 

Investigation 2:

What happens when we replace "cos" with "sin":

Suppose we now have the equations:

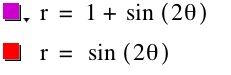
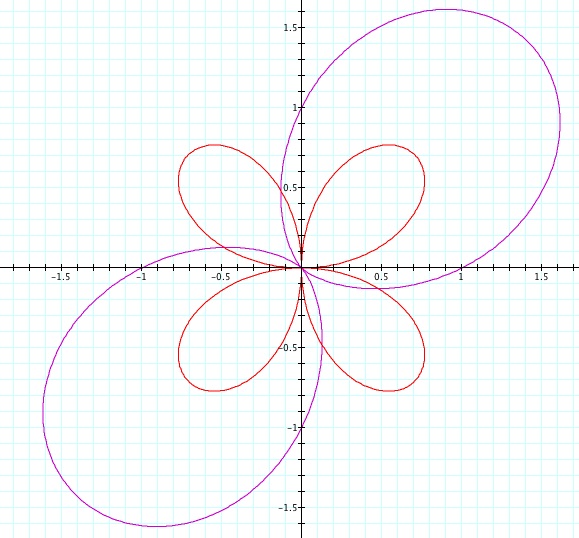
When we change our trig function from "cos" to "sin," our graph rotates 45 degrees or π/4 in radians. This rotation of 45 degrees stays consistent with any value of "k," odd or even. Above we see the graph of the sin functions when k=2. Now let's see the graphs when k=3,4,5:

Graph of sin functions when k=3:

 

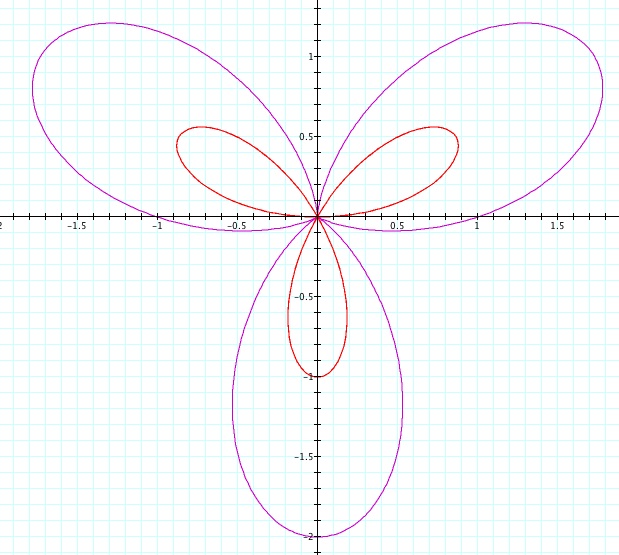
Graph of sin functions when k=4:

 

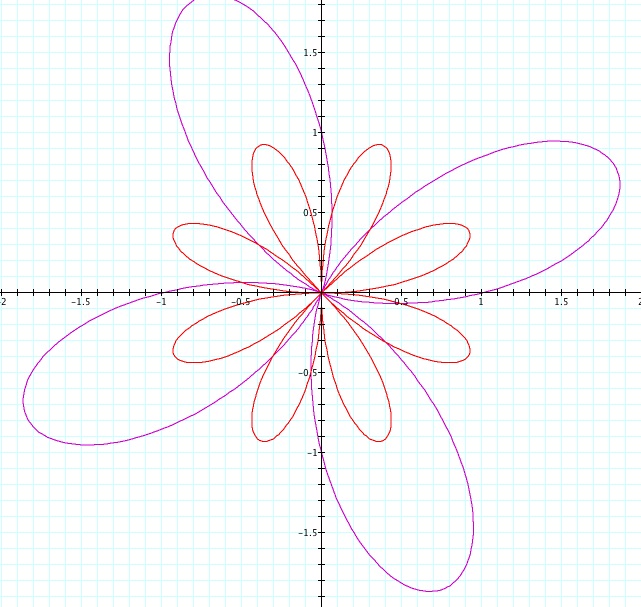
Graph of sin functions when k=5:

Hence, the number of clovers stays consistent with the earlier graphs of cos functions, but the two things that did not stay consistent when switching to sin functions was the rotation of the figure by 45 degrees and the axes of symmetry change.